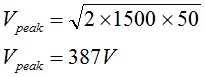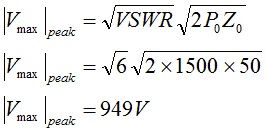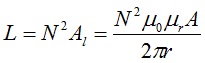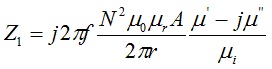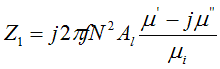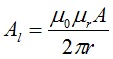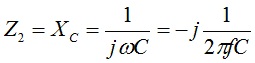Introduction
Differential and common modes on transmission lines were introduced in Part I [1] of this article. The use of baluns to mitigate common mode currents on transmission lines that feed dipole antennas were also discussed. Finally, the use and placement of common mode chokes were introduced.
In this installment, the work of Gustav Guanella [2] is chronicled, followed by Joe Reisert’s improvements [3] to Guanella’s original design. Next, the construction of a common mode choke is presented that includes data for the coax used. Finally, some analyses are performed to predict the performance of two common mode chokes, and graphical results are provided.
Guanella Balun
Gustav Guanella was a Swiss electrical engineer and prolific inventor. His name is associated with more than 200 patents [4]. One of his inventions was a new transformer design that appeared in The Brown Boveri Review in September 1944 [5]. Figure 1 depicts [6] his new transformer/coupler model. Two parallel, closely spaced wires are wound on an insulating core at a). The input and output center-tapped transformers at b) provide a means to separate and recombine differential and common mode currents in this embodiment. Differential, symmetrical currents (solid lines), i1, travel along a section of balanced transmission line at designation, A. Common Mode, asymmetrical currents (dotted lines), i2, travel along an alternate path through an RF choking inductor at designation, B.
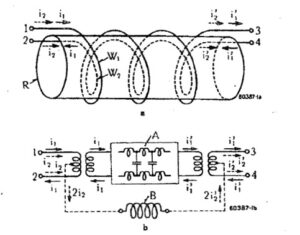
Figure 1. Guanella’s Double Wire Coil System with Equivalent Diagram. A two-wire transformer is wound on an insulating core at a). An equivalent circuit diagram is provided at b). The center-tapped transformers at b) provide a means to separate the differential current, i1, from the common mode current, i2. At A, the differential current passes through a balanced transmission line section, while at B, the common mode current is routed to a choking inductor. Reproduced with permission from ABB Ltd – The Brown Boveri Review, Vol. XXXI, No. 9, Sept. 1944, pp. 327 – 329, Baden, Switzerland.
Guanella’s simplest embodiment for a 1:1 balun is depicted in Figure 2 [7]. The inductance of the windings serves to suppress the asymmetrical (common mode) currents so that a balanced transmission line carrying symmetric currents in differential mode to the left may be connected to an unbalanced transmission line carrying asymmetric currents in common mode to the right. This transformation is possible regardless of frequency. Furthermore, Guanella demonstrates [8] that placing the inputs of more than one coil system in series on one side and in parallel on the other side can be used to implement transformations in the ratio of 1:N2 where N is the number of coil systems placed in series-parallel. For N=1, we have 1:12, which is just 1:1, as shown in Figure 2. An improvement to this design is presented in the next section.
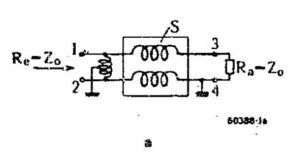
Figure 2. Guanella’s model for a 1:1 balun for transforming symmetrical balanced (differential mode) transmission line at the left to an unbalanced asymmetrical (common mode) transmission line to the right where one side is grounded. The suppression of the asymmetrical currents by the choking inductance of the windings makes it possible to connect balanced to unbalanced line. Reproduced with permission from ABB Ltd – The Brown Boveri Review, Vol. XXXI, No. 9, Sept. 1944, pp. 327 – 329, Baden, Switzerland.
Joe Reisert’s Improved Broadband Balun
Joe Reisert, W1JR, presented an interesting variation of the Guanella transformer in the September 1978 issue of Ham Radio magazine [9]. Unbalanced operation was described in Part I of this article which models the coax as a 3-wire transmission line. Symmetric differential mode currents will flow on the center conductor and inner shield, the desired mode of operation. However, there is nothing to prevent current from flowing on the outside of the coax shield since the outside and inside are conjoined at the antenna center insulator.
The Guanella design winds balanced wire transmission line on an insulating core, but there is no reason why an unbalanced coax cannot be wound on an insulating core to obtain a similar result. W1JR describes earlier versions of this design wound on ferrite rods [10]. In this configuration he states that there have been reports of “frequency sensitivity” over the decade in frequency required. There is also the problem of loss that will be a function of the magnetization admittance for the ferrite material chosen. Lower permeability materials will result in lower core losses but higher flux leakage. Rods will result in higher flux leakage than a toroid. Lower permeability cores will require more turns to achieve the same impedance as toroids for similar materials. Now that #31 with initial permeability, μi, of 1500 and #43 material with initial permeability, μi, of 800 are available, they are logical choices for HF use. The impedances of the windings will vary as a function of frequency, but 11 or 12 turns on these cores are adequate to provide a great deal of common mode attenuation over the HF frequency range. The core losses as a function of the number turns on toroid ferrite cores were the subject of an earlier article [11].
Figure 3 illustrates W1JR’s improved design [12]. This device is suitable for use as an antenna balun as illustrated. When both ports are terminated with coaxial connectors, the device is suitable for use as a common mode choke. To paraphrase the Traub Manufacturing Company slogan [13], Joe Reisert’s balun is “Often imitated, frequently duplicated.”
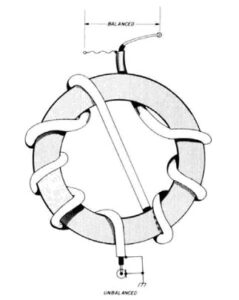
Figure 3. W1JR’s Improved Broadband Balun. Eight turns are depicted in this graphic. Since the crossover winding passes through the core, it counts as a single turn. This 1:1 balun will transform unbalanced coaxial transmission line to the balanced feed point of a dipole antenna. If the balanced side is connectorized, the balun becomes a common mode choke. If sufficient inductance is present for the outer coax shield, the asymmetric common mode currents on the outer coax shield are suppressed. Reprinted with permission from the September 1978 issue of Ham Radio magazine, © CQ Communications, Inc.
Fabrication
Coax Properties
Two coaxial cable types under consideration for common mode choke fabrication are RG-303/U [14] and RG-400/U [15].
Voltage Specifications
We consider RG-303/U that was recommended in Joe Reisert’s article [16] and RG-400/U that was used in the construction of two common mode chokes described in this article. Both are compact PTFE coaxial cables characterized by working voltages of 1400V RMS, or 1980V peak. Assuming that the cables are perfectly matched to the transmitter and the antenna, the peak voltages on the cables are found to be,
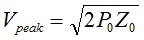
where:
P0 is the transmitter power – for example 1500W
Z0 is the characteristic impedance of the coaxial cable, 50 ohms
Thus,
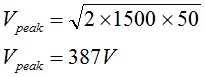
The peak voltage on the line for a matched system is 387 volts for 1500W. This does not challenge the voltage specification of the coaxial cable.
Next, let’s consider the case where the antenna is mismatched to the line. As an example, a 6:1 VSWR will be considered. For this case the magnitude of the maximum peak voltage on the transmission line may be as great as [17],
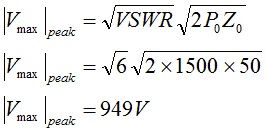
This voltage is well within the specification limits for both coaxial cable types with the proviso that the connectors have been properly installed on the cable ends.
Minimum Coaxial Cable Bend Radius
The bend radius of the coaxial cables should be considered for both cable types. For RG-303/U the minimum bend radius [18] is specified to be 2” (50.8mm) while for RG-400/U a value of 1” (25.4mm) applies [19]. Because of the sharp bends required around the stacked FT240 toroidal ferrite cores during the winding process, it would appear that neither coax meets the bend radius requirement. Since Teflon will deform, it is expected that, over time, the center conductor will migrate from the center of the dielectric.
Power Handling Capability
This discussion would not be complete without a few words about the power handling capability for the ferrite used. The #31 and #43 ferrite materials possess high permeability properties. They are also lossy.
A discussion of power handling capability for ferrites was provided in a previous article [20]. This topic may not be ignored for ferrite use at high power. The higher the permeability, the more lossy the material will be. Of the two materials cited in this article, #31 with an initial permeability of 1500 has the highest loss. It is absolutely essential that the choking impedance be as high as possible and that the material loss be as low as possible to prevent overheating. PTFE coax is unlikely to melt, but ferrite cores have been known to shatter due to thermal runaway once the Curie temperature is reached. This is a safety concern. Contrary to what has been written on the web, ferrite devices used in power applications should always be enclosed and properly ventilated if required.
The heating effect is due to the outer shield being wrapped around the ferrite core which has a choking effect. The inner coax transmission line operating in differential mode by itself is not the cause of heating. The outer coax shield must be treated as a third common mode transmission line from a standpoint of dissipative loss when wrapped around the core.
Construction Details
Seven connectorized common mode chokes were constructed for use in transmission lines and for use at the operating location, as required. Without line chokes common mode currents are apt to find their way back to the operating location on the coax shield. Common mode currents can create reception, equipment and operator problems. For maximum effect the choking impedance should be located at a voltage node in the transmission line where the wave impedance of the standing wave is low [21]. If a dipole antenna is in use, a choking balun should also be located at the feed point.
The line chokes were constructed on stacked cores of FT240-31 and FT240-43 material. The literature recommends both for EMI suppression [22]. Eleven turns of RG-400/U coax were wound on each of the stacked cores with a Joe Reisert, W1JR, crossover winding in the center. Each choke was housed in a Bud Industries PN-1323 box [23]. Holes were drilled in the housings with a Milwaukee step drill [24]. Step drills are essential for boring holes in plastics and metals, and they are well worth the initial investment. Connections are made to the coax shield using the technique best illustrated in Figure 4. A short length of insulation is removed from the coax, the coax braid is tinned and the short piece of buss wire is wrapped around the braid and soldered. If PTFE coax is used, nothing will melt. The free end of the buss wire is bonded to the UHF connector flange with a solder lug and #4-40 hardware. The buss wire should be as short as is practical.
Figure 4. Connecting to the Coax Shield. The recommended method for connecting to the coaxial shield is pictured. Since the dielectric is PTFE, it will not melt when the braid is tinned. Where required, a short length of shrink tubing may be used to cover the exposed shield.
Common Mode Choking Impedance Predictions
Common mode choking impedances were estimated for stacked cores consisting of 2 x FT240-31 and 2 x FT240-43 ferrite toroid materials. Eleven turns of RG-400.U were wound on each stacked core. The choking impedance for each was calculated as a function of frequency for each core. Permeability data was obtained as a .csv file for each core at the Fair Rite website.
Since the inductance of a toroid is calculated from the value of the magnetic flux by the expression,
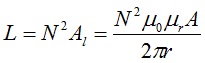
where:
N is the number of turns wound
Al is the inductance per turn in units of Henries, H
μ0 = 4π x 1E-07 is the permeability of free space in units of H/m
μr is the relative permeability constant, dimensionless (relative to μ0)
A is the cross-sectional area of the core in units of m2
r is the average radius of the core in units of m.
the complex impedance may be calculated from,
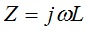
where:
L is the inductance in units of Henries, H
ω = 2πf the angular frequency in units of radians/s
f is the frequency of operation in units of Hertz, Hz, or s-1
Since the value of Al is based upon the value of μi, the initial permeability at 10 kHz, the permeability value must be modified to include the complex permeability. This is key to deriving the frequency dependence of impedance based upon the complex permeability [25].
Thus, we may write:
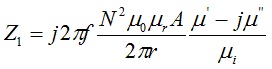
where:
μi is the initial permeability, dimensionless
μ’ is the real part of the complex permeability, dimensionless
μ” is the imaginary part of the complex permeability, dimensionless
If the value of Al happens to be provided by the ferrite manufacturer, the expression for Z is simplified to,
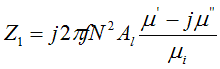
If the value of Al is not readily available, it may be calculated from,
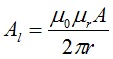
A value, 2 pf, for an interwinding capacitance was incorporated into the calculation by placing it in parallel with the toroid winding. It’s a guess. Recall that,
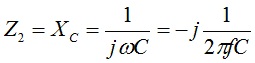
Applying the formula for parallel impedances,
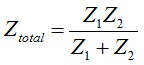
the choking impedances were plotted for 11 turns on 2 x FT240-31 and 2 x FT240-43 stacked ferrite toroid cores. The calculations are quite tedious, so some automation is essential. An Excel spreadsheet can be generated after .csv files have been downloaded with frequency-dependent, complex permeability data from the manufacturer, Fair Rite. The results appear in Figures 5 and 6, respectively. Depending upon the provenance of the ferrite used, actual results may vary by ± 20%.
If a nanoVNA is available, the impedance of the outer shield winding may be measured. Then, the resonant frequency of the common mode choke, which is the zero crossing of the reactance, may be determined. These points are visible in Figures 5 and 6 at 6.2 and 7 MHz, respectively. Once the resonant frequency has been determined through measurement, the capacitance value in the analysis for Z2 can be adjusted so that the frequency of resonance for the analysis data matches the measured data.
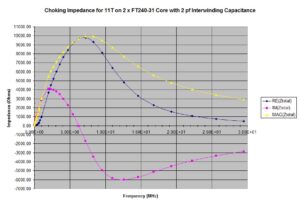
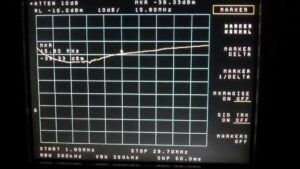
Figure 5. Choking Impedance for Stacked FT240-31 Cores. Eleven turns were modeled on 2 x FT240-31 cores. A 2 pf capacitor is modeled in parallel with the winding to represent the interwinding capacitance. The choking impedance is sensitive to the number of turns and an interwinding capacitance that tends to reduce the impedance with increasing frequency.
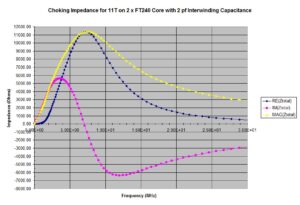
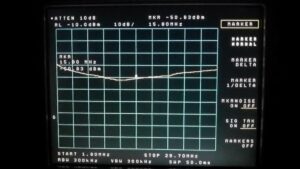
Figure 6. Choking Impedance for Stacked FT240-43 Cores. Eleven turns were modeled on 2 x FT240-31 cores. A 2 pf capacitor is modeled in parallel with the winding to represent the interwinding capacitance. The choking impedance is sensitive to the number of turns and an interwinding capacitance that tends to reduce the impedance with increasing frequency.
Performance measurements for the common mode chokes described in this article are presented in Part III.
References
[1] Martin Blustine, K1FQL, Differential and Common Modes on Transmission Lines – Part I, July 25, 2022. https://www.n1fd.org/?s=Common+Mode
[2] Biography, Gustav Guanella, Wikipedia, https://en.wikipedia.org/wiki/Gustav_Guanella
[3] Joe Reisert, Simple and Efficient Broadband Balun, Ham Radio, September 1978, pp. 12 – 15.
[4] Biography, Gustav Guanella, op. cit. https://en.wikipedia.org/wiki/Gustav_Guanella
[5] Gustav Guanella, New Method of Impedance Matching in Radio-Frequency Circuits, The Brown Boveri Review, V. XXXI, No. 9. pp. 327 –329. https://library.e.abb.com/public/dadf14b477e54194ba7613a3aae11e7a/bbc_mitteilungen_1944_e_09.pdf?x-sign=lWb6zmbVjwsVidyeEEIqKcRGbQm7nu2SHtvRAO9177wOzUNw0KaE8CNmiu5MYIfM
[6] Ibid, p. 327.
[7] Gustav Guanella, op. cit., p. 328.
[8] Gustav Guanella, op. cit., p. 328.
[9] Joe Reisert, op. cit.
[10] Joe Reisert, op. cit., p. 13.
[11] Martin Blustine, K1FQL, Power Losses and Dissipation in Various Ferrite Devices – Part II, August 12, 2022. https://www.n1fd.org/2022/08/12/ferrite-loss-2/
[12] Joe Reisert, op. cit., p. 13.
[13] Traub Manufacturing, https://www.quora.com/Who-coined-the-phrase-Often-imitated-never-duplicated
[14] Belden RG-303/U, https://catalog.belden.com/index.cfm?event=pd&p=PF_84303
[15] Belden RG-400/U, https://edesk.belden.com/products/techdata/EUR/MRG400.pdf
[16] Joe Reisert, op. cit., p. 14.
[17] Martin Blustine, K1FQL, Worst Case Standing Wave Voltage on a Transmission Line, August 1, 2022. https://www.n1fd.org/2022/08/01/standing-wave-voltage/
[18] Belden RG-303/U, op. cit.
[19] Belden RG-400/U, op. cit.
[20] Martin Blustine, K1FQL, Power Losses and Dissipation in Various Ferrite Devices – Part II, op. cit. https://www.n1fd.org/2022/08/12/ferrite-loss-2/
[21] Chuck Counselman, W1HIS, Common-Mode Chokes, YCCC, April 6, 2006, p.13. https://remoteqth.com/img/ZAW-WIKI/cmcc/CommonModeChokesW1HIS.pdf
[22] https://www.fair-rite.com/product-category/suppression-components/round-cable-emi-suppression-cores/
[23] https://www.budind.com/product/nema-ip-rated-boxes/pn-series-nema-box/ip65-nema-4x-box-pn-1323/ – group=series-products&external_dimension
[24] https://www.homedepot.com/b/Tools-Power-Tool-Accessories-Drill-Bits/Milwaukee/Step/N-5yc1vZc248ZzvZ1z0y9ih
[25] Owen Duffy, VK1OD, A Method for Estimating the Impedance of a Ferrite
Cored Toroidal Inductor at RF, December 29, 2015.
https://owenduffy.net/files/EstimateZFerriteToroidInductor.pdf
Figure 1 – Feeding the Common Mode Choke in Common Mode. A resistive power divider was constructed that consisted of paralleled 51-ohm resistors to make two 25.5-ohm resistors. The center conductor of the choke coax and the choke coax shield were fed with in-phase signals from the spectrum analyzer tracking generator.
Figure 2 – Recombining the Common Mode Signals. Similarly, a resistive power combiner was constructed at the choke output that consisted of paralleled 51-ohm resistors to make two 25.5-ohm resistors. The in-phase signals from the center conductor of the choke coax and the choke coax shield are recombined and fed to the spectrum analyzer input. The shield from the input coax and output coax is bridged with a piece of #16 AWG copper wire as shown. 
Figure -. Suppression of a 2 x FT240-31 Line Choke. The ferrite material favors the lower bands but the overall suppression is inferior when compared to that of the 2 x FT240-43 line choke. Deconstruction of the choke may disclose some defects in materials or construction. Only a single choke of this type was constructed.
Figure 4 – Suppression of a 2 x FT240-43 Line Choke. The ferrite material favors the higher bands but the overall suppression is superior when compared to that of the 2 x FT240-31 line choke. Fortuitously, several chokes of this type were constructed.
