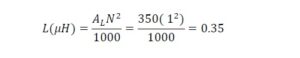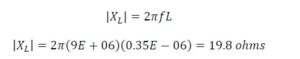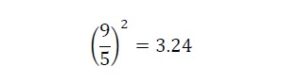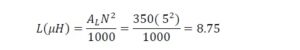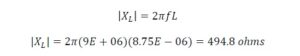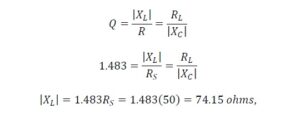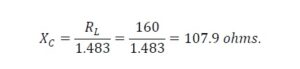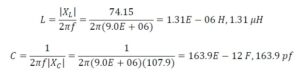All posts by Martin Blustine

I studied physics and went on to work in infrared optics, millimeter wave and microwave engineering until retirement. My interests lie in teaching, music, radio astronomy, infrared systems and microwave and antenna engineering. I enjoy writing technical papers about ham radio topics. When I am not operating CW, I enjoy homebrewing ham gear and restoring vintage HP and Agilent test and measurement equipment.
Homebrewing

A Simple Set of QRP Calibration Mismatches That You Can Build

I enjoy homebrewing, and when it was time to calibrate the Stockton Bridge for measuring forward and reflected power in my QRP rig, I realized that I didn’t have a set of mismatches that could be used for that purpose. A set of mismatches is also useful for checking an SWR meter, or a nanoVNA. There are off-the-shelf mismatches that you can buy to test your nano, but they do not provide the power handling capability that this design does.

If you would like to get started with PCB design, this might be a perfect project to begin with. I am not endorsing any particular PCB design tool that you might find online, but I have found that EasyEDA is easy to learn.

The mismatches that I describe here can be used for QRP. All resistors in the design are 51-ohms and 2 Watts. Since we are not using 50-ohm resistors, this will result in a small error. Also, the layout is distributed (spread out), and this will result in a bit of extra capacitive reactance for the larger mismatches. SMA connectors were chosen because all of the RF interconnections within my QRP rig consist of RG316 terminated with SMA connectors.

Figure 1 is the schematic of what was built. It seemed pretty easy to construct the mismatches from a single value of resistor, but there is nothing to stop you from building mismatches from one or two parallel values of different resistors. What I have here seemed like a good idea because it made calculations simpler, and it resulted in power-handling capability large enough for any QRP project that I envisioned. Values of 3.0:1, 2.5:1, 2.0:1, 1.5:1 and 1.0:1 were chosen as data points for the Stockton Bridge that I was calibrating. For continuous operation at 5W, a cooling fan is recommended, particularly for the 1.0:1 load bank as it has the fewest number of resistors.

Figure 1. A Simple Set of Mismatches. Use of a single resistor value, 51-ohms and 2 Watts throughout, makes construction easy and economical. Use of series and parallel combinations result in higher power dissipations. Please click on the figure to enlarge it.

Figure 2 shows the virtual 3-D layout as provided by the EasyEDA PCB layout tool. The tool shows you what you are going to get once the PCB is assembled. The EasyEDA library is extensive, and it provides additional capability to import manufacturer’s symbols and footprints not already in the library. Although this set of mismatches was built as a PCB, there is nothing to stop you from building the same design on a piece of copper-clad perforated board.

Figure 2. Calibration Mismatches 3-D View. EasyEDA provides a 3-D viewer so that you can see what the final product will look like before the PCB is fabricated and before the PCB is populated. The mismatch values are shown near the SMA connectors. Please click on the figure to enlarge it.

Figure 3 shows the shows the final product after PCB fabrication and population. It closely matches what is shown in Figure 2.

Figure 3. As-Built Calibration Mismatches. The actual PCB closely resembles the 3-D model shown in Figure 2. The overall dimensions of the completed board are 6.50” x 3.60” including the connectors. Please click on the figure to enlarge it.

S11 values for the mismatches were measured from 1.8 to 29.7 MHz and stored on an old MFJ-226 Graphical Analyzer. The values were converted to rectangular form in Excel spreadsheets to facilitate calculations. Smith Charts were also plotted. In order to make this article more concise, the Smith Charts are provided in the Appendix that follows.

If you would like the S11 data in the form of Excel, please contact me. The spreadsheets contain all of the formulas required to convert S11 magnitude and angle to other useful forms including S11 rectangular, impedance rectangular, impedance polar, VSWR and return loss.

If you would like the Gerber file for PCB fabrication, you may also contact me.  I will not be providing any bare boards, although you may wish to pool a PCB order to distribute the shipping costs among a few hams. For the JLCPCB supplier, the minimum number of boards is 5.

Appendix A. Smith Charts

Figure A-1. Smith Chart 1.0:1 Mismatch.

Figure A-2. Smith Chart 1.5:1 Mismatch.

Figure A-3. Smith Chart 2.0:1 Mismatch.

Figure A-4. Smith Chart 2.5:1 Mismatch.

Figure A-5. Smith Chart 3.0:1 Mismatch.

General, Homebrewing

Impedance Matching to an 8-Pole Quasi-Equiripple (QER) Crystal Bandpass Filter

Introduction

An amateur radio transceiver will often require at least two crystal bandpass filters; one for SSB, and another for CW operation. This article discusses impedance matching techniques for a SSB crystal filter to be used in a homebrew QRP transceiver. For a CW filter, the bandwidth would be narrower, but the design process for a matching network would be the same.

Crystal Filter Project Description

When this project began in 2017, there was nothing but a bag of fifty 9 MHz crystals ordered from DigiKey[1]. In retrospect, it might have been more cost-effective to buy a few more of these crystals to get the job done for SSB and CW filters.

Not wanting to bother measuring the crystal motional parameters to enter into DISHAL[2][3]; a simpler approach was adopted[4] which was to sort the crystals into batches of crystals differing in frequency by not more than 10 percent of the desired filter bandwidth. For an SSB filter having a bandwidth of 2.7 kHz, the prescription is to find crystals that are all within 270 Hz of one another. For a 500 Hz wide CW filter, the task becomes more difficult because it requires crystal matching to better than 50 Hz.

Subsequently, I built a crystal oscillator circuit for the purpose of sorting crystals into batches. I chose to follow the advice of Charlie Morris, ZL2CTM, who had done the same [5]. I used the receiver in my rig to measure the frequencies of oscillation by zero beating the crystal oscillator against a signal generator since I didn’t own a frequency counter until recently. I also zero-beat the crystal oscillator against an SDR receiver BFO to compare the crystals to one another. There was lots of advice to be found online about “this and that” including how to handle the crystals with tweezers to avoid heating them up[6].

For the batch of 50 Citizen crystals[7] that I sorted, I was not successful in obtaining a set of 10 crystals that met the frequency matching criteria. Thinking that I didn’t want to invest in more crystals, I decided to look for a filter kit whose crystals had already been sorted[8] and whose capacitors had been chosen. There are at least two sources of supply for crystal filter printed circuit boards; one requires the purchase of a set of matched crystals[9] and features places for onboard matching, and another requires an external matching network[10]. I bought a bare board from the former to build a CW filter and a fully populated board from the latter for the SSB filter. A picture of the beautifully made filter from the latter is shown in Figure 1. The filter was characterized by the supplier and came with the following test data:

  • Center Frequency: 8.997500 MHz
  • 3 dB Bandwidth: 2.7 kHz
  • In/Out Impedance: ~160 ohms
  • Insertion Loss: 2.65 dB
  • Bandpass Ripple: < 1.2 dB

Figure 1. An 8-Pole Quasi-Equiripple (QER) Bandpass Filter. SMA male connectors were added to the device as supplied. No matching networks were furnished for the filter input or output. The supplier advises that matching may be achieved through the use of matching transformers or L-matching networks. Please click on the figure to enlarge it.

Crystal Filter Matching With Matching Transformers

Assuming that the supplier has already determined the best match by placing potentiometers in series with the input and output of the filter to optimize the filter shape, I relied upon their measurement of ~160 ohms as a starting point.

This is a commonly used technique. The potentiometers are adjusted for the best filter passband and stopband shape by sweeping the filter with a nanoVNA, or by viewing the passband response on a spectrum analyzer using an integral tracking generator. Once the potentiometers have been adjusted for the best passband and stopband shape, the potentiometers are measured and 50 ohms is added to each value. This is because the source impedance during the measurement is assumed to be 50 ohms as is the load impedance.

Since I wanted to match the crystals to a 50 ohm system for my QRP rig, I knew that the impedance ratio of the matching network had to be 50:160, or 1:3.2, at the input and 160:50, or 3.2:1, at the output. Since I was going to try a matching transformer for the first pass, I knew that this impedance ratio was not the same as the required turns ratio. To obtain the turns ratio, we must take the square root of the impedance ratio, 3.2, to obtain 1.79. Thus, the turns ratio is 1-turn to 1.79-turns at the input and 1.79-turns  to 1-turn at the output.

It is not possible to build a transformer with this turns ratio since only a whole number of turns is possible. Also, we must have a sufficient number of turns on the primary to avoid loading the source. A rule-of-thumb is to ensure that the impedance of the smallest winding is > 5 times the lowest impedance that must be matched. That dictates that the smallest winding must have an impedance of 50 ohms x 5 = 250 ohms at 9 MHz. Next, we use an iterative approach to find the smallest number of turns that will meet our requirements. We do this because the more turns we add, the more the inter-turn capacitance increases. This adds to the complexity of the matching solution. We must always use integer numbers of turns for both windings, so we will seldom get the exact ratio required.

Example 1 – 1-Turn to 2-Turns

If we were to round the 1:1.79 turns ratio to a whole number ratio, we ask, how close would a 1-turn to 2-turn transformer come to meet our requirements? First, we look at the impedance ratio for 1T:2T. It is simply the square of the 2-turn winding, or 4. So, this 1T:2T winding will match 50 ohms to 200 ohms which isn’t a very good match at all. Please, recall that we needed to match 50 ohms to 160 ohms. We also look at the impedance of the smallest winding to see if the magnitude of the impedance is > 5 x 50 ohms, or 250 ohms.

Assuming that the winding is purely inductive, it has an impedance magnitude given by

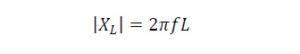where,

Since the transformer ferrite material is FT37-43, how is the inductance for a 1-turn winding determined?

The manufacturer of the ferrite frequency supplies a factor for a specific core that, when multiplied by the square of the number of turns, will approximate the inductance of the winding. This factor is called AL.

If we study the manufacturer’s data[11] for a FT37-43 core having part number 5943000201, we learn that the AL factor is 350 nH/N2 +/-20% for #43 ferrite of FT37 dimensions.

When we have AL, the formula for inductance for a single turn in units of µH, after converting from units of nH to µH, is given by,

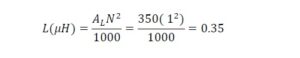
where,

Finally, the value of the magnitude of impedance is calculated from,

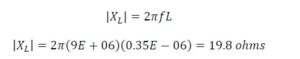
This value is not large enough to meet our reactance requirement of > 250 ohms.

Once you have mastered this process, you may wish to employ an online calculator[12].

We could repeat this exercise for other turn ratios by repeating the process, but to save some time, let’s try a ratio of 5-turns to 9-turns in the next example. The reader should try some other turns ratios to better understand the process. For example, try a ratio of 3-turns to 5-turns to see what happens.

Example – 5-Turns to 9-Turns

A ratio of 5-turns to 9 turns results in an impedance ratio of,

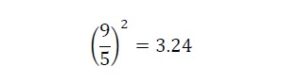
which is close the value, 3.2, that was calculated initially, and

Let’s try this turns ratio of 5T:9T because it results in a value that is close to the desired 160 ohms.

Next, we repeat the process by calculating the reactance of the 5-turn winding since it is the smaller of the two windings. We must first calculate the inductance,

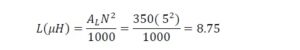
From this value of 8.75 µH, we now calculate the magnitude of the inductive reactance at 9 MHz from,

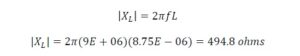
This result is greater than our 250-ohm requirement, and it will work for us.

Matching Transformer Simulation

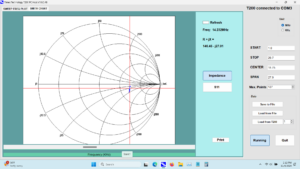
The matching transformer may be simulated using RFSim99[13]. The transformer model is shown in Figure 2. It is modeled as an ideal transformer for which there is no frequency component or coupling factor, k. A rectangular plot of the return loss of the transformer is shown in Figure 3. Since there is no frequency component, the return loss of 44.14 dB is flat for all frequencies. The turns ratio of 5T:9T results in a match between 50 ohms and 162 ohms, a slightly imperfect match for the 160-ohm load. A Smith Chart plot of the match is shown in Figure 4. If the photo is magnified, the cursor appears very close to the center of the chart for all frequencies.

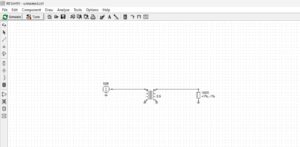
Figure 2. Matching Element Consisting of an Ideal Transformer. A turns ratio of 5T:9T is an imperfect match to 160 ohms. A perfect match would be to 162 ohms. Please click on the figure to enlarge it.

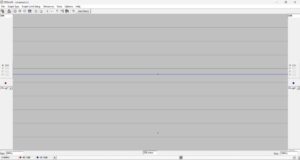
Figure 3. Return Loss for the Ideal Transformer Matching. Since there is no frequency component to an ideal transformer, the match is flat over all frequencies. The return loss is 44.14 dB due to the slight turn ratio mismatch. Please click on the figure to enlarge it.

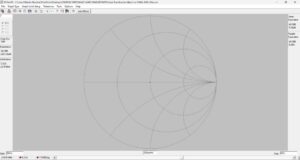
Figure 4. Smith Chart View. Since the simulation is for an ideal transformer possessing no frequency dependence, the cursor resides near the very center of the chart over a wide span of frequencies. Please click on the figure to enlarge it.

Matching Transformer Hardware

Thinking that the matching transformers might be permanently connected to the crystal filter; a printed circuit board was designed using EasyEDA, an online PCB design tool. The Gerber file for the design was transferred electronically to a fabricator, JLCPCB, in Hong Kong, and finished boards were delivered by DHL within 5 days.

The 3D virtual design is shown in Figure 5. Two Fair Rite FT37-43 toroidal cores were wound with #27 AWG magnet wire, each with a 5-turn primary and a 9-turn secondary. They were wound in no particular sense in mind except to match symbol pattern imprinted on the silk screen.  Spoiler Alert: If you are like me, there is a 50-50 chance of winding it the right way the first time around.

Figure 5. Matching Transformer PCB Design. Notice that the center pins of both SMA connectors are routed to the dotted pads. The center conductor from the top SMA connector is routed under the toroid. The undotted pads above the toroid are ground pads for both windings. Thus, the windings, though unequal in number, happen to be wound in the same sense. The EasyEDA design tool provides these 3D virtual views of the finished product. There is a massive library of symbols contributed by users, so there is seldom a need to draw any of them. The only caveat is for multi-pin connectors. There are instances where the schematic model pinouts do not match the PCB graphics model pinouts, and EasyEDA advises the designer to verify the models before using them. Please click on the figure to enlarge it.

The resulting transformers are shown in Figure 6. No difficulties were encountered with assembly and the PCBs and transformers worked exactly as intended.

Figure 6. Matching Transformer Assembly. The two windings just happen to be wound in the same sense to match the silkscreen outline on the printed circuit board. The smaller winding has been wound right over the larger winding. Once assembled it is easy to lose track of which end of the transformer is 50 ohms and which end is 160 ohms. One should always mark the 50-ohm end with indelible ink. Male SMA connectors are used to avoid unnecessary cables and adapters between modules. Please click on the figure to enlarge it.

Crystal Filter Measurements

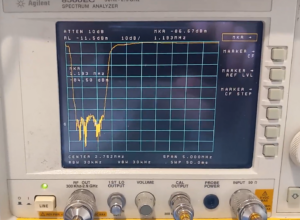
The passband and stopbands of the matched filter were measured with a spectrum analyzer with an integral tracking generator. A tracking generator is a signal source whose RF output follows the tuning of the spectrum analyzer. It could just as well have been measured with a nanoVNA that does the same thing, but I do not own one. The values of center frequency, bandwidth and insertion loss agree quite closely with the values provided by the supplier. The tracking generator outputs -10 dBm, so everything is measured relative to this power level. The coaxial cables that connect the tracking generator to the filter and the filter to the spectrum analyzer are 18” in length. No padding attenuators have been inserted in either the input path or the output path of the device under test (DUT). The test setup is shown in Figure 7. The through-path loss is zeroed out before inserting the device under test which in this case includes the crystal filter with its two matching transformers.

Figure 7. Test Setup For Filter Passband and Stopband Measurements. Nearly identical matching transformers have been placed at the input and output ports of the filter. The transformer to the left steps up the impedance from 50 ohms to 162 ohms, while the transformer to the right steps down the impedance from 162 ohms to 50 ohms. Neither of the 18” interconnecting coaxial cables has been padded. The through-path losses have been zeroed out before inserting the device under test. Please click on the figure to enlarge it.

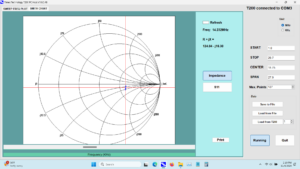
The filter passband was swept with the tracking generator to evaluate the insertion loss of the filter. The losses of cables and adapters have been zeroed out. The insertion loss shown in Figure 8 agrees closely with that measured by the supplier ~ 2.65 dB. The filter center frequency differs slightly from that reported by the supplier, but that is accounted for by the state of instrument calibration and instrument settings.

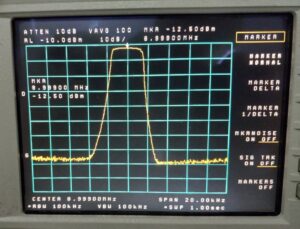
Figure 8. Crystal Filter Swept Measurement. The filter passband was swept with the tracking generator to evaluate the insertion loss of the filter. The losses of cables and adapters have been zeroed out. The insertion loss agrees with that measured by the supplier at band center ~ 2.65 dB. Please click on the figure to enlarge it.

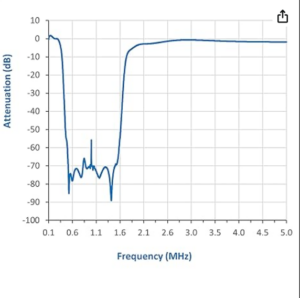
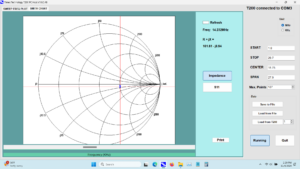
Finally, the -3 dB passband of the filter was measured with the spectrum analyzer. This measurement has been captured in Figure 9. The filter bandwidth is measured to be 2.9 kHz which compares favorably with the supplier’s measurement of 2.7 kHz although it is a bit wider than was hoped.

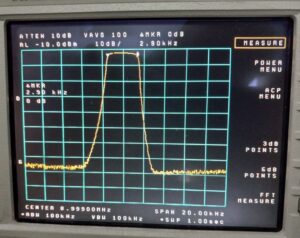
Figure 9. Crystal Filter 3 dB Passband Measurement. The bandwidth was reported by the supplier to be 2.7 kHz, but this measurement shows that it is 2.9 kHz. This is somewhat wider than was hoped, but this filter will be used. The steeper skirt at the high side of the response is characteristic of these filters. Please click on the figure to enlarge it.

Except for matching transformers, no alterations have been made to the filter other than to solder connectors to the PCB. The passband ripple is supposed to improve by bonding the crystals together with a soldered strap. From the results pictured, there doesn’t seem to be much utility in trying this. There is always the risk of damaging the filter by soldering to the crystal packages. The filter high side and low side skirt selectivities are as expected; the high side being steeper than the low side. Although this filter does not have skirts as steep as those found in a commercial SSB filter, it is adequate for this QRP rig.

Use of L-Matching Networks to Effect a Match

To demonstrate the method, the design of an L-matching network will be provided in this section. This same methodology has been used before in this blog[14]. For completeness, the topology choices are repeated in Figure 10.

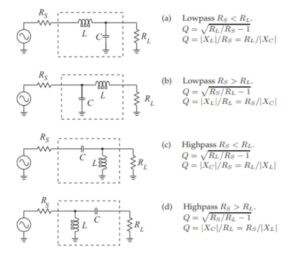
Figure 10. Topology Choices for L-Matching Networks. A topology is chosen depending upon whether a low-pass or high-pass configuration is required, and if Rs < RL , or if RS  >  RL . These topologies may be used to map and match the entire complex impedance plane. Reproduced under CC BY-NC by permission of Michael Steer, North Carolina State University. Please click on the figure to enlarge it.

The impedance level to which we wish to match, 160 ohms, is greater than the source impedance, 50 ohms, Rs < RL, and a solution topology (a) is selected, for the sake of example. It happens to be the low-pass topology that will pass DC current. This will place the inductor in series with the source and a capacitance in parallel with the crystal filter load impedance.

The shunt or parallel matching element, as it may be called, will always be closest to the larger of the two impedances. This mnemonic helps us to remember the topology choices. Whether the low-pass or high-pass topology is chosen will depend upon whether the component values are realizable, easily adjusted, and whether we want the network to pass DC current.

There is no need to design a different network for the filter output because the network is reciprocal meaning that it works the same way in reverse, and the mnemonic still applies. The output topology would be a shunt capacitor at the filter and a series inductor towards the load. You might prove this to yourself as an exercise by choosing the topology used for RS > RL  since, this time, the high source impedance will be 160 ohms and the load impedance will be 50 ohms.

From Figure 10 (a) we have,

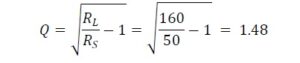
and

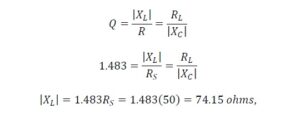
and

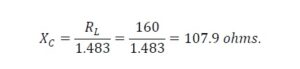
Solving for the values of the inductance and the capacitance, we have,

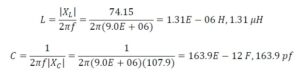
The matching network consists of a series inductance of 1.31 µH and a shunt capacitance of 163.9 pf.

Once you have mastered this process, you may wish to employ an online calculator[15].

L-Network Simulation

We can use RFSim99 to prove that we have achieved a match with this L-network. The model used for the simulation is shown in Figure 11. A rectangular plot of the return loss is shown in Figure 12. The Smith Chart of the match is shown in Figure 13.

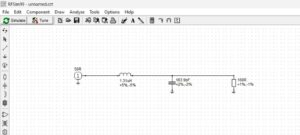
Figure 11. L-Matching Network Model. The 160-ohm input load impedance of the crystal filter can be matched to the 50-ohm source impedance with an L-network consisting of a series inductance of 1.31 µH and a shunt capacitance of 163.9 pf. Please click on the figure to enlarge it.

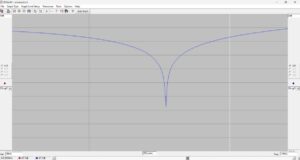
Figure 12. Return Loss of the L-Matching Network. The sweep is from 7 MHz to 11 MHz. The return loss for a very simple L-matching network at the design frequency of 9 MHz is better than 67 dB. Please click on the figure to enlarge it.

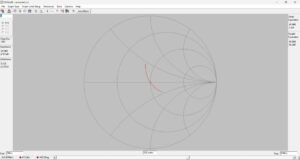
Figure 13. Smith Chart for the L-Matching Network. The sweep is from 7 MHz to 11 MHz. A perfect match is displayed on the Smith Chart at 9 MHz with the cursor positioned at the very center of the chart. Please click on the figure to enlarge it.

Conclusions

It has been demonstrated that matching to a crystal filter, commercial or homebrew, is not difficult. The techniques used for transformer and L-matching are ones that have been demonstrated previously. It is hoped that the reader will try both techniques for practice if only by following the examples that have been worked on.

References

[1] DigiKey, 701 Brooks Avenue South, Thief River Falls, MN.

[2] Milton Dishal, “Modern Network Theory Design of Single-Sideband Crystal Ladder Filters,” Proceedings of the IEEE, Sep 1965.

[3] Dishal Download: https://www.minikits.com.au/downloads

[4] Wes Hayward, Designing and Building Simple Crystal Filters, QST July 1987, pp. 24-29.

[5] Charlie Morris, ZL2CTM, https://www.youtube.com/watch?v=Ur7Cze-X0zo

[6] Jerry Hall, W0PWE, https://www.qsl.net/w0pwe/HB/Xtal_Osc.html

[7] Citizens Part Number HC-49/U-S9000000ABJB

[8] https://kitsandparts.com

[9] Ibid. https://kitsandparts.com/crystals.php

https://kitsandparts.com/XF.php

[10] Mostly DIY RF, https://mostlydiyrf.com/qer

[11] Fair Rite, PN 5943000201, https://fair-rite.com/product/toroids-5943000201/

[12] https://toroids.info/FT37-43.php

[13] James Butler, AD5GG, https://www.ad5gg.com/2017/04/06/free-rf-simulation-software/

[14] Martin Blustine, K1FQL, https://www.n1fd.org/2022/06/11/l-matching-networks/

[15] John Wetherell, author, Impedance Matching Network Designer, https://home.sandiego.edu/~ekim/e194rfs01/jwmatcher/matcher2.html

 

Antennas, Featured, General

Matching to the Complex Load Impedance of a Shortened, Non-Resonant Antenna – Part III – Radiation Efficiency, Ground Reflective Loss, and Antenna Efficiency

Introduction

Part III of this series is lengthy. It provides the reader with several worked examples in EZNEC that may be helpful. Consequently, the remainder of the topics intended for this installment will be postponed to Part IV. These include methods for hand-calculating radiation resistance, antenna capacitance, antenna ohmic losses from the skin effect, and antenna feed point voltages.

For those of you who would like to use EZNEC, Roy Lewallen, W7EL, has generously made it available, free of charge, to anyone wishing to download it[1].

This section results from a post to the QRZ Technical Forum[2] in which I asked W7EL if he would review the three EZNEC cases that I planned to use to obtain the parameters required to calculate the radiation efficiency for a short, non-resonant vertical antenna.

I received a lengthy response from W7EL and thought-provoking comments from Mike Mladejovsky, WA7ARK[3], and from Dan Maguire, AC6LA, author of AutoEZ[4]. In his response, since it had not been considered, W7EL provided the method for computing the ground reflective loss for the antenna. When the Radiation Efficiency and Reflective Loss are taken together, this shortened, non-resonant vertical is quite inefficient. As will be seen in Part IV, the efficiency is worsened by the resistance of any inductive matching elements that will be necessary at the feed point of this highly reactive antenna.

This article has been largely reorganized to place the results up front and to place the EZNEC models in the Appendices. Appendix A offers a tutorial on how to generate antenna radials. Appendix B, with included comments, provides screenshots of all of the EZNEC cases that contribute to the results.

EZNEC File Recommendations

Based upon their collective recommendations, I altered the three files that I had posted to QRZ Technical Forum: Antennas, Feedlines, Grounding & Towers[5] to eliminate any error messages and departures from the EZNEC User’s Manual by:

1.      Moving the source upward to a higher segment of the vertical antenna radiator as shown in the Source Descriptions.

1.      Modeling the ground radials at least 0.001 wavelengths above the ground[6] for the NEC-2D engine. (NEC-2D does not provide for buried radials, but NEC-5 does. Since almost no one has a license for NEC-5, all of the calculations in this paper employ the NEC-2D engine.)

2.      Following WA7ARK’s recommendation to reduce the radial lengths to match the height of the antenna.

3.      Reducing the number of segments in all conductors by using the guidelines provided in the EZNEC User’s Manual[7]. It states that 10 segments are a reasonable number per half wavelength for pattern/gain analysis work. For accurate impedance calculations, 20 segments per half wavelength are reasonable.

4.      Ignoring the effects of dielectric insulation losses for radial wires because they are negligible.

These recommendations having been taken into account; seven cases were run. For those of you who are merely interested in the numbers, the cases are summarized in Figure 1, while the feed point impedances are summarized in Figure 2.

Some interesting results are calculated along the way, and some generalized results for antenna efficiency are provided at the end of this article once reflective losses have been addressed.

There is sufficient information provided in Figure 1 to build the models for the seven cases and to reproduce the results tabulated in Figure 2. It is hoped that the reader will follow along to learn more about EZNEC and what it contains. It is also a good exercise for learning how to generate ground radials, and that is covered.

Figure 1. Table of Case Parameters. Seven cases were run to determine the antenna efficiency of a shortened, non-resonant vertical. Please click on the figure to enlarge it.

Figure 2. Case Summary. Results from seven cases are summarized. This table contains everything required to approximate the antenna efficiency of a shortened, non-resonant vertical antenna. Please click on the figure to enlarge it.

Radiation Efficiency, Ground Reflective Loss, and Antenna Efficiency
Computation of the Radiation Resistance
For Case 1B, Plate 4, VSWR Plot, the impedance of the antenna for this case without conductor losses is 3.658 – j519.6 ohms. Compare this impedance with that of Case 1A, Plate 4, with conductor losses, 3.679 – j519.6 ohms. The difference is 21 milliohms which should approximate aluminum radiator RF resistance. Since conductor loss has been removed for Case 1B, and the ground is perfect, the real part of this impedance, 3.658 ohms, should approximate the radiation resistance of this antenna.

Computation of the Ground Loss

For Case 2A, Plate 4, VSWR Plot, the impedance of the antenna for this case is 7.092 – j534.5 ohms. Since Case 1A, real part 3.679 ohms, contains only the resistive losses, and Case 2A, real part 7.092 ohms, contains the resistive and ground losses, the difference should be the ground loss, 3.413 ohms.

Computation of the Ohmic Losses

If we subtract the real part of Case 2B from the real part of Case 2A, the result is 0.026 ohms, the sum of the radiator and radial resistances. If we subtract the real part of Case 3B from the real part of Case 3A, the result is 0.026 ohms. The result is consistent as it should be for the antenna with its radials.

Computation of the Radiation Efficiency

Now that we have the radiation resistance, 3.658 ohms, the ground loss, 3.413 ohms, and the conductor resistance, 0.026 ohms, we can estimate the radiation efficiency of the antenna which does not include any matching inductor loss or any dielectric loss at this time.

The radiation efficiency for this antenna is approximately 51.5%. Converting to dB, we have,

Ground Reflective Loss

If Case 1C is run with Real/MININEC ground, conductor ohmic loss and ground medium, the average gain is -6.01 dB and this is 5.98 dB down from -0.03 dB for Case 1A with perfect ground and conductor ohmic loss. This is due to the ground reflective loss.

Antenna Efficiency

Assuming that there is a matching network at the base of the antenna to provide a good match between 50-ohms and this highly reactive antenna, we will, for the moment, ignore ohmic losses in the matching network. We will also ignore polarization losses that increase as the cosine of the angle between the actual and desired polarization.

After running Case 2B for Real/High Accuracy Ground, we calculated the radiation efficiency and converted 51.5%, to dB to obtain -2.88 dB. When combined with the ground reflective loss, we obtain:

If we compare this result with that of Case 2A average gain that includes the ohmic and reflective loss minus the Case 1A, perfect ground with ohmic loss, we get -8.83 dB:

There is agreement between these two results to within 0.03 dB.

Converting the former to percent:

Converting the latter to percent:

By any measure, this shortened, non-resonant vertical antenna is inefficient.

Final Check

As a final check, if Case 1B with Perfect Ground, zero conductor loss, and with a real part of 3.658 ohms is compared with Case 3B, Real/High Accuracy ground, zero conductor loss, near perfect conductivity at 12 S/m, and with a real part of 3.709 ohms, we conclude that with a difference of only 51 milliohms, there is general agreement. In other words, if Real/High Accuracy ground cases are made to look like near Perfect ground cases by increasing their ground conductivity, the results should be fairly consistent.

References

[1] Lewallen, Roy, W7EL, author of EZNEC Pro+ v. 7.0. https://www.eznec.com/

[2] QRZ Technical Forums, Antennas, Feedlines, Grounding & Towers. K1FQL post: Modeling of Shortened Vertical Antennas in EZNEC, pp. 1 – 3. https://forums.qrz.com/index.php?threads/modeling-of-shortened-verticals-in-eznec.899108/

[3] Mladejovsky, Mike, PhD, WA7ARK, Prof. of EE, Retired, University of Utah.

[4] Maguire, Dan, AC6LA, author of AutoEZ: AutoEZ for EZNEC automation. https://ac6la.com/autoez.html

[5] QRZ Technical Forums, Antennas, Feedlines, Grounding & Towers, op. cit., pp. 1-3.

[6] Lewallen, Roy, EZNEC User’s Manual for EZNEC Pro+ v. 7.0, p. 84. https://www.eznec.com/ez70manual.html

[7] Ibid, p. 64.

Appendix A

Generating Ground Radials in EZNEC – Example

For those who have not generated radials in EZNEC, it is not difficult. We begin with the EZNEC Control Panel as shown in Figure A1. For computations, the frequency has been set to 3.6 MHz. Please note that we begin with a single wire of 10 segments. There is one Source, a Real/High Accuracy has been selected, and the Wire Loss has been set to zero. This means that the radiating element and the ground radial ohmic losses have been set to zero. A ground conductivity of 0.005 S/m and ground dielectric constant of 13 has been selected. Under Plot Type, select 3D. Please try the azimuth and elevation patterns, too.

Figure A1. The EZNEC Control Panel. The frequency has been set to 3.6 MHz, the ground type has been set to Real/High Accuracy, and the wire loss has been set to zero. A ground conductivity of 0.005 S/m and a ground dielectric constant of 13 have been selected. Please click on the figure to enlarge it.

The next step is to access the Wires list from the Control Panel by clicking on Wires. A single line is seen in the wire list, Figure A2. The wire radiating element is, in fact, a piece of tubing that is 31.75mm (1.25”) in diameter. The tubing is vertical and runs from End 1 at Z = 0.083m to End 2 at Z=7.551m. If we subtract the two, we see that the vertical radiating element length is 7.468m, the actual antenna length. The lower end of the antenna has been raised to 0.083m (8.3cm) above ground. This is because the radials must be elevated to 0.001 wavelength above ground. The wire segmentation is set to 10 from guidance provided in the EZNEC User’s Manual.

Figure A2. The Wire List. Once selected, the first entry is for the vertical antenna radiator which extends from 0.083m (8.3cm) above ground to 7.551m above ground. The total length of the radiator is 7.468m (24.5 ft). The radiating element consists of an aluminum tube that is 31.75mm (1.25”) in diameter. The conductor resistivity has been set to zero and is not shown. There is no insulation on the tubing, so the dielectric constant is set to 1. The wire segmentation has been set to 10. See text. Please click on the figure to enlarge it.

The next step is to add radials to the Wire List, Figure A3. The radials have to be elevated by 0.083m (0.001 wavelength) to meet the minimum height requirement for the EZNEC NEC-2D engine. Line 2 is the first radial. Since the radials run horizontally, End 1 is at Z=0.083m and End 2 is at Z=0.083m. The radial runs from Y=0 at End 1 to Y=7.468m at End 2. The diameter of #14 AWG wire is 1.638mm. The X-coordinates have been set to zero because they are not used.

Figure A3. Adding the First Radial Wire. The first radial wire is added to the wire list on line 2. It consists of #14 AWG wire that is 1.638mm (0.0645”) in diameter. It is uninsulated, so its dielectric constant is set to unity. The radials are placed at the minimum required height, 0.001 wavelength, above ground for the ENZNEC NEC-2D engine which does not allow for buried radials. At 3.6 MHz, the wavelength is 83.28m, so the minimum radial height is 8.3cm, or 0.083m. Notice that the radial has been made equal to the height of the antenna, 7.468m (24.5’), and both ends of the radial are 0.083m above ground. The wire segmentation has been set to 10 per the EZNEC User’s Manual. Please click on the figure to enlarge it.

For the sake of example, 10 equally spaced radials will be generated automatically by EZNEC. To do this, a dropdown dialog box is opened under Create, Figure A4. From this list, Radials… is selected.

Figure A4. Dropdown Dialog Box. Radials is selected in the dropdown menu. Please click on the figure to enlarge it.

Upon selecting Radials…from the dropdown menu, another dialog box opens, Figure A5. The first line asks us what the first line for the radial prototype is, and the number 2 is entered because it is where the information for the first radial wire has been entered. The second line asks what the last wire in the prototype group is. It is 11 because the first line for the radiator description is counted and 11 is the last radial wire. The third line is just the total number of radial wires, 10. Those lines having been entered; OK is chosen.

Figure A5. Create Radials Entry. Since the radial wire entries begin with wire 2 in the wire table, the first wire in prototype group is 2. Since there are 10 radial wires, the last wire in the prototype group is 11. The total number of radials is 10. Please click on the figure to enlarge it.

Ten equally spaced radials are generated in the Wires Panel, Figure A6.

Figure A6. Ten equally spaced radials are listed in the wire table from line 2 to line 11. Notice that the radial on line 5 points in the direction opposite to the one on line 2. Please click on the figure to enlarge it.

Once the wire table is produced, the Source Panel is opened by the user, Figure A7. The source is placed as close to End 1 of Wire 1 as possible. If we remember that for the EZNEC NEC-2D engine, sources are placed in the center of line segments, let’s see what happens if we try to place the source at 0% from Wire 1, End 1. EZNEC automatically places the source at 5% from End 1. Since there are 10 segments, and 20 half-segments, the center of the first segment is 5% as is shown.

Figure A7. Source Location. The source location is specified in the sources list. As a first guess, we try placing the source 0% from Wire #1, End 1. EZNEC moves it to a point 5% from Wire 1, End 1. This is the center of the first of ten wire segments that make up the vertical. We recall from the EZNEC User’s Manual that sources are placed at the center of wire segments for the NEC-2D engine. Please click on the figure to enlarge it.

Next, in the Control Panel, a VSWR plot is selected. An error message is produced as shown in Figure A8. What’s wrong?

Figure A8. Segmentation Check Error. Everything seems alright, so what’s wrong? Please see text. Please click on the figure to enlarge it.

EZNEC is trying to tell us that the source in the middle of the first segment is still too close to the radial wires. That is because it knows that the first radial and Wire 1, End 1, have been placed 0.083m (8.3cm) above the ground surface. If the source is raised 11% from End 1, EZNEC increases the location of the source to 15%. That is the center of segment 2, Figure A9. EZNEC has to place sources in the middle of segments. We obtain a visual of where it is located when we ask to see what the antenna looks like. If we don’t like the elevated source location, we can try adding more segments to the radiating element so that the source location moves downward even though it will still be centered in Wire 1, Segment 2. Then, if we run a VSWR computation, we can observe if it has a large effect on the impedance, or if there is a diminishing return, as is stated in the EZNEC User’s Manual. Please try changing the number of segments in Wire 1 to see what happens.

Figure A9. Sources List. As a second try, we move the source 11% from Wire 1, End 1. This places the source in Segment 2. EZNEC reinforces this by moving our choice 15% from Wire 1, End 1, and into Segment 2. We obtain a visual on where it is located when we ask to see what the antenna looks like. Please click on the figure to enlarge it.

We may select a segmentation check from the Options dropdown menu that is accessible from the Control Panel, Figure A10. It confirms that the error message has vanished.

Figure A10. Segmentation Check. Once the source has been moved to a segment that is acceptable to EZNEC, the segmentation check shows ok. Please click on the figure to enlarge it.

At this point, let’s see what the antenna looks like, Figure A11, by clicking on View Ant on the Control Panel. The source is 1-1/2 segments from the plane of the radials. We’ll see what happens.

Figure A11. Antenna View. A vertical radiating element is shown with its 10 radials. Both have been elevated to 0.083m (8.3cm) above ground. Please note the position of the source (the tiny red circle) which is plainly visible in the center of the second segment of the vertical radiating element. EZNEC enforces this because we have elevated everything off the ground by 0.001 wavelength. Please click on the figure to enlarge it.

A VSWR Plot may be selected and run from the Control Panel. A dialog box opens, and the frequency range is entered as well as the frequency step interval, Figure A12. Although it is seldom noticed, individual frequencies may be listed in a text file, and these may be called by checking the box that says Read Frequencies From File. This is useful for displaying VSWR data over multiple bands. A named text file must be stored where EZNEC can find it, preferably in the same folder where the EZNEC file has been saved. It is called up by selecting the file name. Please try it. Only discrete frequencies need to be listed. Frequency Step size is not required.

Figure A12. SWR Sweep Parameters. This data entry panel provides start/stop limits for the frequency scan and step granularity. It also provides a means for selecting a frequency data file in which discrete frequency data for a single frequency band, or multiple bands is stored. Please click on the figure to enlarge it.

Once we are happy with the Frequency Selection and Frequency Step, Run is selected, and a VSWR Plot appears. Since the antenna has not been matched, and the antenna is highly reactive, the VSWR is astronomically high > 100:1, Figure A13. If we click right on the SWR Plot at 3.6 MHz, the tiny, circular cursor moves to the center of the chart, and the parameters for the calculations appear for the antenna at 3.6 MHz right below the plot. We observe that the impedance of this antenna is computed to be 7.618 – j629.4 ohms. Since this is a short, non-resonant vertical, the real part of the impedance is expected to be low when compared to the ~36.5 ohm real part of a 0.25-wave vertical, resonant monopole above perfect ground. The 629.4 ohm capacitive reactance, indicated by the minus sign on the imaginary part, arises from the fact that the antenna is very short at 3.6 MHz. In Part IV, it will be shown that high feed point reactances give rise to very high voltages, even at low power. The subject of Reflection Coefficient was discussed in detail in a previous post, Blustine, Martin, K1FQL, N1FD post, Worst Case Standing Wave Voltage on a Transmission Line, August 1, 2022. https://www.n1fd.org/2022/08/01/standing-wave-voltage/

Figure A13. SWR Plot. The SWR is >100:1 for this unmatched non-resonant, vertical antenna. The impedance is 7.618 – j629.4 ohms. The high reactive part gives rise to very high voltages at the antenna feed point. A matching element is required at the feed point to reduce the SWR to a level that can be handled by an automatic antenna tuner, either remote or local. Please click on the figure to enlarge it.

Next, we may request a 2D or 3D antenna pattern from the Control Panel under FF Plot. Let’s request a 3D antenna pattern so that EZNEC will calculate the average antenna gain from the plot, Figure A14.

Figure A14. 3D Antenna Pattern. EZNEC plots the 3D antenna pattern for us while computing the average gain for the antenna that will be displayed on the Control Panel once the 3D antenna pattern has been run. Please click on the figure to enlarge it.

If we reduce or close the 3D plot, an average gain computation appears at the bottom of the Control Panel, Figure A15. The average gain for the entire pattern is -6.55 dB. This average is computed from several discrete samples. There is a note that says that the Model contains loss. Even though the conductor ohmic losses are zero, there is still ground loss.

Figure A15. Average Gain Computed from the 3D Pattern. The gain is displayed at the bottom of the Control Panel. Even though conductor losses have been set to zero, the model displays the comment Model contains loss. This is because EZNEC has also computed the ground loss for this antenna. Please click on the figure to enlarge it.

If we were to change the Ground Type in the Control Panel to Perfect, we see that this ground loss disappears because it has not been included in the model, Figure A16. Subtracting -0.01 dB from -6.55 dB, we conclude that the average gain is -6.54 dB for the Real/High Accuracy ground type that includes ground loss. The reason that the average gain for perfect ground does not show as zero is that the calculation is performed by sampling at several discrete points on the pattern.

Figure A16. Average Gain Once Ground Type Is Set to Perfect. Reflective loss is not included in this model. The reason that the Average Gain does not say zero is that the average gain is computed for several discrete points on the pattern. Please click on the figure to enlarge it.

Appendix B

Case 1A: 24.5′ Vertical W. Radiator Ohmic Loss, W.O. Radial  Ohmic Loss, W.O. Radial Insulation Dielectric Loss

Figure B1. Case 1A, Plate 1, Control Panel for EZNEC. A 24.5′ Vertical with radiator ohmic loss, without radial ohmic loss, and without radial wire insulation dielectric loss has been modeled. The ground type is perfect, and there are no ground radials present. Please click on the figure to enlarge it.

Figure B2. Case 1A, Plate 2, Wire List. Only the aluminum radiator with ohmic loss is present. The ground type is perfect, and there are no ground radials present. Please click on the figure to enlarge it.Figure B3. Case 1A, Plate 3, Source Location Description. Note that when there is perfect ground, the source is located near the end of the antenna conductor and close to the ground plane. Please click on the figure to enlarge it.

Figure B4. Case 1A, Plate 4, VSWR Plot. The impedance of the antenna for this case is 3.679 – j519.6 ohms. Please click on the figure to enlarge it

Figure B5. Case 1A, Plate 5, 3D Antenna Pattern. The pattern extends down to the perfect ground conductor. Please click on the figure to enlarge it.

Figure B6. Case 1A, Plate 6. Average Gain Computation. Under Plot Type, 3D is selected. After the 3D pattern has been run, the average gain is computed and reported by EZNEC at the bottom of the Control Panel. Note that for a perfectly conducting ground with conductor loss for the radiating element, the average gain is -0.03 dB. Please click on the figure to enlarge it.

Case 1B: 24.5′ Vertical W.O Radiator Ohmic Loss, W.O. Radial Ohmic Loss, W.O. Radial Insulation Dielectric Loss

Figure B7. Case 1B, Plate 1, Control Panel for EZNEC. A 24.5′ Vertical without radiator ohmic loss, without radial ohmic loss, and without radial wire insulation dielectric loss has been modeled. The ground type is perfect, and there are no ground radials present. Please click on the figure to enlarge it.

Figure B8. Case 1B, Plate 2, Wire List. Only the aluminum radiator without ohmic loss is present. The ground type is perfect, and there are no ground radials present. Please click on the figure to enlarge it.

Figure B9. Case 1B, Plate 3, Source Location Description. Note that when there is perfect ground, the source is located near the end of the antenna conductor and close to the ground plane. Please click on the figure to enlarge it.

Figure B10. Case 1B, Plate 4, VSWR Plot. The impedance of the antenna for this case without conductor losses is 3.658 – j519.6 ohms. Compare this impedance with that of Case 1A, Plate 4, with conductor losses, 3.679 – j519.6 ohms. The difference is 21 milliohms which should approximate aluminum radiator RF resistance. Since conductor loss has been removed and the ground is perfect, the real part of this impedance, 3.658 ohms, should approximate the radiation resistance of this antenna. Please click on the figure to enlarge it.

Figure B11. Case 1B, Plate 5, 3D Antenna Pattern. The pattern extends all the way down to the perfect ground conductor. This is characteristic of antennas modeled above perfect, or near-perfect ground conductors. Please click on the figure to enlarge it.

Figure B12. Case 1B, Plate 6, Average Gain Computation. Under Plot Type, 3D is selected. After the 3D pattern has been run, the average gain is computed and reported by EZNEC at the bottom of the Control Panel. Note that for a perfectly conducting ground without conductor loss for the radiating element, the average gain is -0.01 dB. When compared to Figure B6, Case 1A, Plate 6, we may infer that the aluminum radiator loss accounts for an additional 0.02 dB of average gain loss. Please click on the figure to enlarge it.

Case 1C 24.5’ Vertical W. Radiator Ohmic Loss, W.O. Radial Ohmic Loss. W.O. Radial Insulation Dielectric Loss to Compute Reflective Loss

Up to now, only conductor ohmic losses and ground losses have been considered for computing radiation efficiency. There is another type of loss present – reflective loss. This is not to be confused with reflected power which is a different matter. Reflective loss is wasted electromagnetic energy that scatters off the ground and does not propagate in the intended direction.

W7EL, explains in QRZ Technical Forums, Antennas, Feedlines, Grounding & Towers, op. cit., p. 2, that reflections occur far beyond the expanse of any practical radial field that we might have. Consequently, reflective loss has little or no effect on the feed point impedance. The way to separate the reflective loss from other losses is discussed in this section.

Real/MININEC ground uses Real ground for the ground reflective calculation, but not for ground ohmic loss because it uses perfect ground for the current and impedance calculation. Consequently, it provides a means of isolating the ground reflective loss.

Case 1A is repeated with Real/MININEC ground, no radials, radiator ohmic loss, 0.001 S/m ground conductance, and ground dielectric constant 7 to find the average gain. We’ll call it Case 1C. This value is adjusted by the gain for Case 1A having perfect ground and radiator conductor loss. The result is the ground reflective loss.

Thus, if we run Case 1A with Real/MININEC ground, called Case 1C, we obtain the following, Figure B13:

Figure B13. Case 1C, Plate 1, Control Panel. Real/MININEC Ground with radiator ohmic loss and ground medium. Real/MININEC uses real ground for the ground reflective calculation but not the ground ohmic loss because it uses perfect ground for the current and impedance calculation. Please click on the figure to enlarge it.

Figure B14. Case 1C, Plate 2, Partial Wire List Real/MININEC Ground with Radiator Ohmic Loss. Please click on the figure to enlarge it.

Figure B15. Case 1C, Plate 3, Source Location Description. Note that EZNEC has permitted us to place the source near the end of Wire 1, Segment 1. MININEC does not enforce the placement of the source at the center of wire segments. Please click on the figure to enlarge it.

Figure B16. Case 1C, Plate 4, VSWR Plot. Real/MININEC Ground with Radiator Ohmic Loss and Ground Medium. The impedance is 3.679 – j519.6 ohms. Please click on the figure to enlarge it.

Figure B17. Case 1C, Plate 5, 3D Antenna Pattern. Real/MININEC Ground with conductor loss and ground medium. Please click on the figure to enlarge it.

Figure B18. Case 1C, Plate 6, Average Gain for Real/MININEC Ground with Radiator Ohmic Loss and Ground Medium. The average gain is -6.01 dB and this is 5.98 dB down from -0.03 dB for Case 1A that had perfect ground, conductor ohmic loss, and no ground medium. This is due to the ground reflective loss. Please click on the figure to enlarge it.

Case 2A: 24.5′ Vertical W. Radiator Ohmic Loss, W. Radial Ohmic Loss, W. Radial Insulation Dielectric Loss

Figure B19. Case 2A, Plate 1, Control Panel. A 24.5′ vertical with radiator ohmic loss, with radial ohmic loss, and with radial wire insulation dielectric loss has been modeled. The ground type is Real/High Accuracy, and there are ground radials present. The soil conductivity is poor and the dielectric constant is low. Please click on the figure to enlarge it.


Figure B20. Case 2A, Plate 2, Partial Wire List. A partial wire list for 60 ground radials is shown. Conductivities for the aluminum radiator and copper ground radials are accounted for as is PVC insulation on the ground radials. The radials have been made the same length as the antenna radiating element. Please click on the figure to enlarge it.

Figure B21. Case 2A, Plate 3, Source Location Description. EZNEC requires the placement of the source in segment 2. Please click on the figure to enlarge it.

Figure B22. Case 2A, Plate 4, VSWR Plot. The impedance of the antenna for this case is 7.092 – j534.5 ohms. Since Case 1, real part 3.679 ohms, contains only the resistive losses, and Case 2, real part 7.092 ohms, contains the resistive and ground losses, the difference should be the ground loss, 3.413 ohms. Please click on the figure to enlarge it.

Figure B23. Case 2A, Plate 5, 3D Antenna Pattern. The pattern is that of a vertical radiator above imperfect ground. Please click on the figure to enlarge it.

Figure B24. Case 2A, Plate 6. Average Gain Computation. Under Plot Type, 3D is selected. After the 3D pattern has been run, the average gain is computed and reported by EZNEC at the bottom of the Control Panel. Notice that in the presence of conductor losses, ground losses and dielectric losses, the average gain is -8.86 dB. Please click on the figure to enlarge it.

Case 2B 24.5′ Vertical W.O. Radiator Conductor Loss, W.O. Radial Conductor Loss, W. Radial Insulation Dielectric Loss

Figure B25. Case 2B, Plate 1, Control Panel. In this model of the 24.5’ vertical with radials above poor conducting soil, we set the conductor loss resistances to zero. Please click on the figure to enlarge it.

Figure B26. Case 2B, Plate 2, Partial Wire List. A partial wire list for 60 ground radials is shown. Notice that the conductor loss resistances for the radiator and the radials have been set to zero. Please click on the figure to enlarge it.

Figure B27. Case 2B, Plate 3, Source Location Description. EZNEC requires the placement of the source in segment 2. Please click on the figure to enlarge it.

Figure B28. Case 2B, Plate 4, VSWR Plot. The impedance reported is 7.066 – j534.6 ohms where the conductor losses have been set to zero. By subtracting the real part, 7.066 ohms, from the real part of Case 2A, Plate 4, 7.092 – j534.5 ohms, we obtain the loss resistances of the radiator and ground radials, 26 milliohms. Now that we have the radiation resistance, 3.658 ohms, the ground loss, 3.413 ohms, and the conductor loss, 0.026 ohms, we can estimate the radiation efficiency of the antenna which does not include any matching inductor loss or any dielectric loss. Please click on the figure to enlarge it.

Figure B29. Case 2B, Plate 5, 3D Antenna Pattern. The plot is that of a vertical radiator above imperfect ground. Please click on the figure to enlarge it.

Figure B30. Case 2B, Plate 6, Average Gain Computation. When the conductor loss is removed, the average gain is reported as -8.84 dB. If we compare this result with that of Case 2A, Plate 6, we see that the difference is only 0.02 dB. This result is consistent with that of Case 1. Please click on the figure to enlarge it.

Case 3A 24.5′ Vertical W. Radiator Conductor Loss, W. Radial Conductor Loss, W. Radial Insulation Dielectric Loss

Figure B31. Case 3A, Plate 1, Control Panel. This time the 24.5’ vertical is operated with radials above highly conductive ground, 12 S/m with a soil dielectric constant of unity. This approximates a near-perfect ground plane even though there are radials present. Please click on the figure to enlarge it.

Figure B32. Case 3A, Plate 2, Partial Wire List. A partial wire list for 60 ground radials is shown. Wire losses are included in this calculation. Please click on the figure to enlarge it.

Figure B33. Case 3A, Plate 3, Source Location Description. EZNEC requires the placement of the source in segment 2. Please click on the figure to enlarge it.

Figure B34. Case 3A, Plate 4, VSWR Plot. The impedance of our 24.5’ vertical with ground radials above nearly perfect ground conductivity is 3.735 – j530.1 ohms. Please note that the real part compares favorably with the result obtained for Case 1A for a 24.5’ vertical with no radials above perfect ground. Please click on the figure to enlarge it.

Figure B35. Case 3A, Plate 5, 3D Antenna Pattern. Note that with ground conductivity set to 12 S/m, the ground conductivity is near perfect. Hence, the pattern appears quite similar to that of the perfect ground plots of Cases 1A and 1B. Please click on the figure to enlarge it.

Figure B36. Case 3A, Plate 6, Average Gain Computation. The average gain computation appears at the bottom of the page for near-perfect ground with conductor losses. Please click on the figure to enlarge it.

Case 3B 24.5′ Vertical W.O. Radiator Conductor Loss, W.O. Radial Conductor Loss, W. Radial Insulation Dielectric Loss

Figure B37. Case 3B, Plate 1, Control Panel. For this exercise, the wire loss is set to zero for the case of nearly perfect ground conductivity. Please click on the figure to enlarge it.

Figure B38. Case 3B, Plate 2, Partial Wire List. A wire list is shown with all conductors set to zero. Please click on the figure to enlarge it.

Figure 39. Case 3B, Plate 3, Source Location Description. EZNEC requires the placement of the source in segment 2. Please click on the figure to enlarge it.

Figure B40. Case 3B, Plate 4, VSWR Plot. With the conductor losses set to zero, the impedance is 3.709 – j530.1 ohms. When compared with Case 3A, 3.735 – j530.1 ohms, we see that the difference in the real parts is 0.026 ohms as we have seen before. Please click on the figure to enlarge it.

Figure B41. Case 3B, Plate 5, Note that with ground conductivity set to 12 S/m, the ground conductivity is near perfect. Hence, the pattern is quite similar to that of perfect ground. Please click on the figure to enlarge it.

Figure B42, Case 3B, Plate 6, Average Gain. The average gain is reported at the bottom of the page for the case of zero wire loss with the antenna with radials above near-perfect ground conductance. If we compare this gain with that of Case 3A, the difference is 0.03 dB which is consistent with previous results. Please click on the figure to enlarge it.